#5. 자료구조

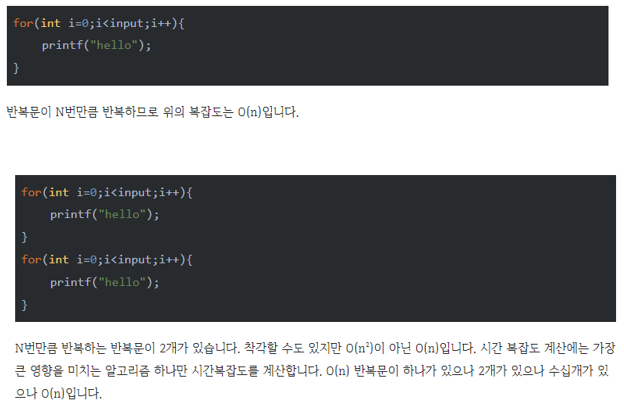
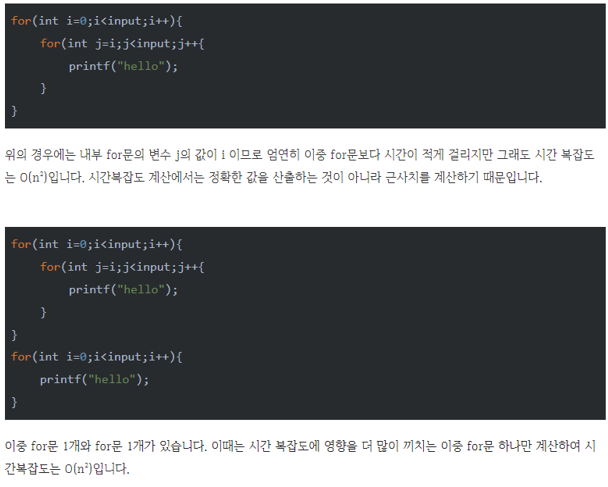
자료구조의 분류
- 자료구조는 크게 선형구조와 비선형구조로 나뉘어짐
- 선형구조: 선형 리스트(배열), 연결 리스트, 스택, 큐, 데크
  - 자료를 구성하는 원소들을 순차적으로 나열시킨 형태
- 비선형구조: 트리, 그래프
  - 하나의 자료 뒤에 여러개의 자료가 존재할 수 있는 형태

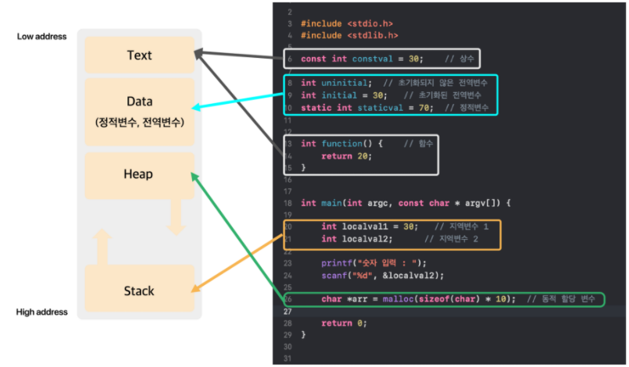
배열
- 인덱스를 가지고 있으며, 순차적으로 데이터가 삽입 삭제될 수 있는 형태의 자료구조
- 데이터를 순차적으로 삽입 삭제 할 때 가장 효과적
- 장점
  - (붙어있어서)인덱스를 사용하기 때문에 검색이 빠르다
- 단점
  - 중간에 삽입 삭제가 어렵다
  - 메모리 크기가 정해져있다

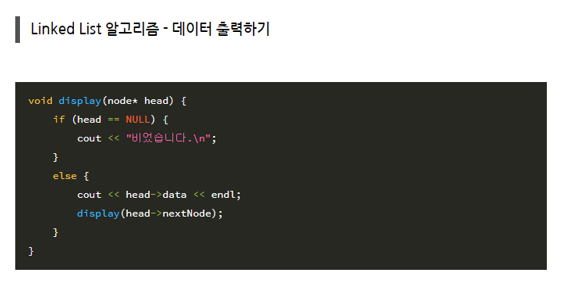
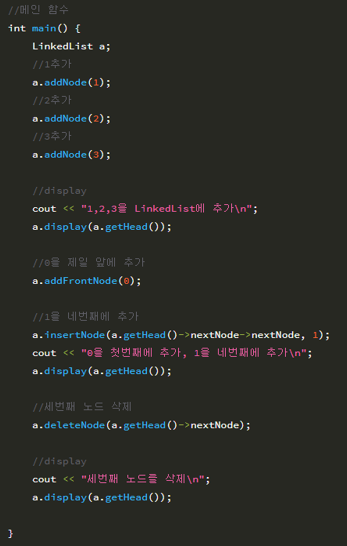
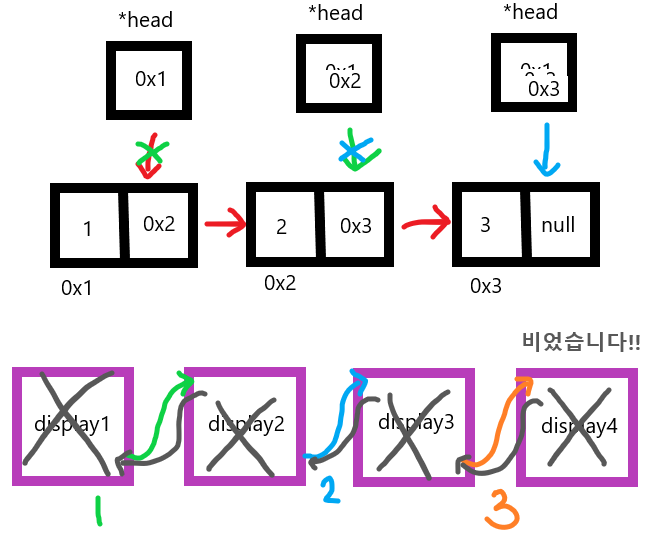
연결 리스트 ->그림 그리고 코드 설명할 수 있도록 무한 반복하기
- 자료들을 임의의 기억 공간에 기억시키되 자료 항목의 순서에 따라 노드의 포인터 부분을 이용하여 서로 연결시킨 자료 구조
- 연결을 위한 포인터 부분이 필요하기 때문에 순차 리스트, 배열에 비해 기억 공간 이용 효율이 좋지는 않다
- 중간 노드의 연결이 끊어지면 그 다음 노드를 찾기 힘들지만, 노드의 연결이 끊어지지만 않는 다면 중간에 삽입 삭제가 용이
- 장점
  - 중간 삽입 삭제가 빠르고 용이하다
  - 연속된 리스트에 데이터들이 일정한 거리만큼 떨어져 저장되는 것과 달리, 데이터 메모리 내의 어느 공간에나 위치할 수 있다
  - 저장과 수정이 간단하기 때문에 데이터의 수를 정확하게 예측할 수 없거나, 데이터의 갯수가 계속해서 바뀌는 경우에 링크드 리스트를 사용하면 좋다
- 단점
  - 검색 속도, 접근 속도가 (배열보다)느리다.
  - Node에 저장되어 있는 nextNode를 따라서 다음 저장된 값을 찾기 때문에 원하는 값의 위치를 찾기 위해서는, 처음부터 순차적으로 탐색해야 하는 단점이 있다.
    - head -> nextNode -> nextNode //세번째 노드 탐색
    - 언제 써?
      - 삽입 삭제가 자주 일어날 때 사용
      - 변동성 심할 때

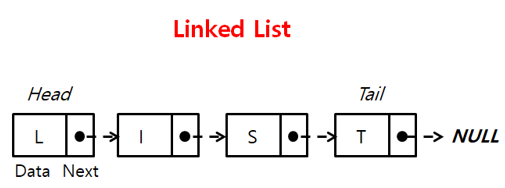
기본 코드

//노드 struct 구현 (data 값과 nextNode가 존재)
struct node {
	int data;
    	node* nextNode;
};

//링크드 리스트 클래스 생성
class LinkedList{
	private: 
    	node* head;
        node* tail;
       
	public:
    	LinkedList() {
        //head와 tail의 포인터를 초기화
        head=NULL;
        tail=NULL;
        }

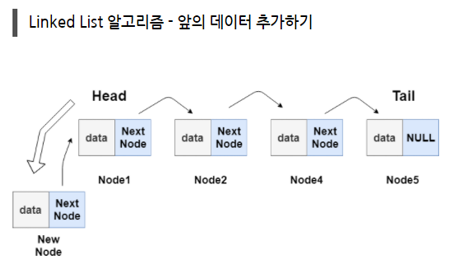
//첫번째의 node 추가
void addFrontNode(int n){
	node* temp= new node;
    	//temp의 데이터는 n
    	temp->data=n;
    
    //LinkedList가 비어있으면
    if(head==NULL){
    
    	//첫 node는 temp
    	head=temp;
    
    	//마지막 node는 temp
    	tail=temp;
    }
    //LinkedList에 데이터가 있으면
    else{
    	//temp의 nextNode는 head
    	temp->nextNode=head;
    	//head는 temp
    	head=temp;
    }
}

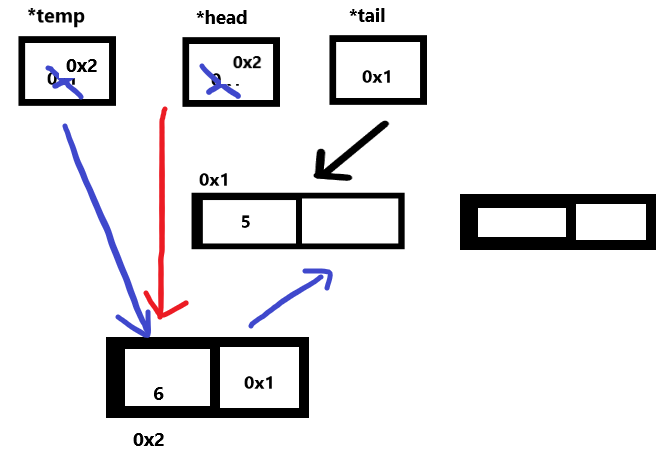
포인터 변수가 주소 가지는 순간 가리키게 된다

=은 ==가 아니라 대입!

대입한다는 것은 덮어 씌운다는 것.

오른쪽 값을 왼쪽에 넣어주는 것임

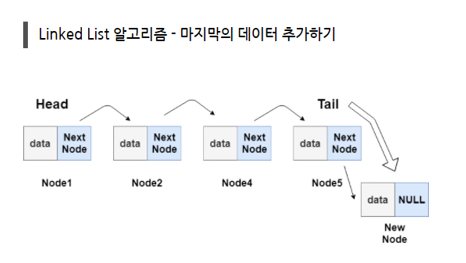
//마지막의 node 추가
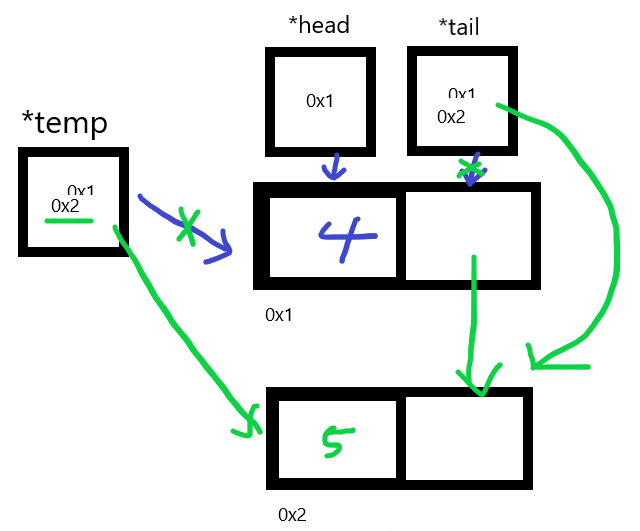
void addNode(int n) {

	node* temp=new node;
    
	//temp의 데이터는 n
	temp->data=n;

	//temp의 nextNode= NULL값
	temp->nextNode=NULL;

	//LinkedList가 비어있으면
    if(head==NULL){
    	//첫 node는 temp;
        head=temp;
        //마지막 node는 temp
        tail=temp;
    	}
    //LinkedList에 데이터가 있으면
    else{
    	//현재 마지막 node의 nextNode는 temp
        tail->nextNode=temp;
        //마지막 node는 temp
        tail=temp;
        
        }
  
  }

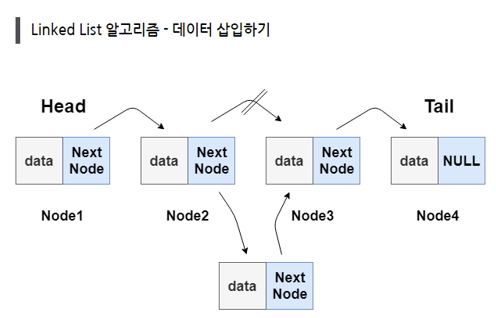
//node 삽입
void insertNode(node* preNode, int n)
{
    node* temp= new node;
    
    //temp의 데이터는 n
    temp->data = n;
    
    //temp의 nextNode 저장
    //삽입 할 앞 node의 nextNode를 temp의 nextNode에 저장
    temp->nextNode = prevNode->nextNode;
    
    //temp 삽입
    //temp앞의 node의 nextNode를 temp로 저장
    prevNode->nextNode=temp;
    
}

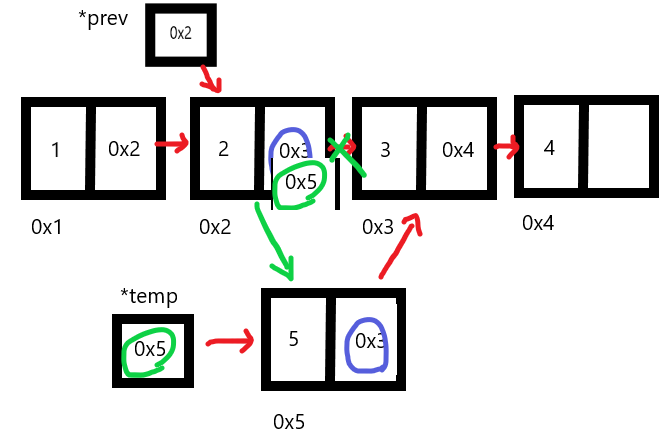
//node 삭제
void deleteNode(node* prevNode)
{

    //삭제할 node를 temp에 저장
    //(삭제할 node의 1단계 전 node의 nextNode)
    node* temp=prevNode->nextNode;
    
    //삭제할 node를 제외
    //(삭제할 node의 nextNode를 1단계 전 node의 nextNode에 저장)
    prevNode->nextNode = temp->nextNode;
    
    //temp 삭제
    delete temp;
 
}

중요한 것: delete temp !!!!!!!!!!!!!!!!!!!!

temp는 위에서 new를 해줬으니 꼭! 지울 때 delete를 해줘야함

동적할당 할 때 이름 없는 변수가 생겨서 가리키고 있는 게 필요.

delete는 주소값을 가지고 있고 주소값 받아서 거기 있는 애를 지워줌.

그래서 temp가 가리키고 있는 0x3번지의 node가(예전에 new로 동적할당한) 지워지는 것이다!

스택(Stack)
- 리스트의 한 쪽 끝으로만 자료를 삽입, 삭제 작업
- 가장 마지막으로 들어온 데이터부터 빠져나가는 후입선출(LIFO) 형식
- 스택의 가장 마지막 삽입 위치를 가리키는 TOP/SP(StackPointer)
- 스택의 가장 밑 바닥을 나타내는 Bottom
- 스택의 자료 입력 명령어인 PUSH
- 스택의 자료 출력 명령어인 POP이 있다

Stack의 특징
1. 먼저 들어간 자료가 나중에 나옴 LIFO(Last In First Out)구조
2. 시스템 해킹에서 버퍼오버플로우 취약점을 이용한 공격을 할 때 스택 메모리의 영역에서 함
3. 인터럽트 처리, 수식의 계산, 서브 루틴의 복귀 번지 저장에 쓰임
4. 그래프의 깊이 우선 탐색(DFS)에서 사용
5. 재귀적(Recursion) 함수를 호출 할 때 사용

큐(Queue)
- 큐는 선형 리스트의 한쪽에서는 삽입 작업이 이루어지고 다른 한쪽에서는 삭제 작업이 이루어지도록 구성한 자료구조
- 가장 먼저 삽입된 자료가 가장 먼저 출력되는 선입선출(FIFO) 방식으로 처리한다
- 가장 먼저 삽입된 자료의 기억 공간을 가리키는 포인터로 삭제 작업이 이루어지는 Front 포인터
- 가장 마지막에 삽입된 자료가 위치한 기억장소를 가리키는 포인터로 삽입 작업이 이루어지는 Rear 포인터
- Queue는 순서를 기다리는 대기 행렬 처리에 사용되거나 운영체제의 작업 스케줄링에 사용된다.

데크(Deque, Double Ended Queue)
- 데크는 Stack과 Queue의 장점을 빼서 따로 구성된 자료구조로, 삽입 삭제가 리스트의 양쪽 끝에서 모두 발생할 수 있는 자료구조
- 입력이 한쪽에서만 발생하고 출력은 양쪽에서 일어날 수 있는 입력 제한과, (입력 제한 데크: Scroll)
- 입력은 양쪽에서 일어나고 출력은 한쪽에서만 이루어지는 출력 제한이 있다.(출력 제한 데크: Shelf)

트리(Tree)
- 트리를 정점(Node)과 선분(Branch)을 이용하여 사이클로 이루어 지지 않도록 구성된 그래프의 특수한 형태
- 트리는 계층 모델로 노드가 N개인 트리는 항상 N-1개의 가지를 갖는다
- 또한 루트에서 어떤 노드로 가는 경로는 유일하다. 트리의 순회는 Pre-Order, In-Order, Post-Order로 이루어진다

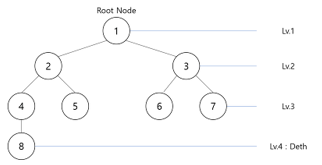
이진 트리(Binary Tree)란?
- 간단히 말하면 모든 트리가 0개 혹은 최대 2개의 자식(왼쪽, 오른쪽) 노드를 갖는 트리를 말함

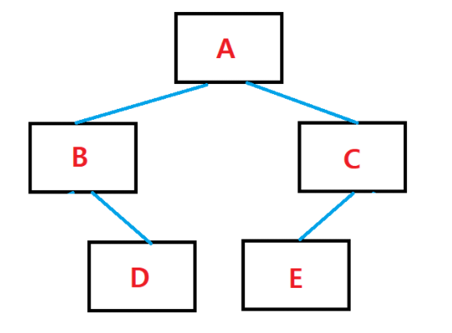
포화 이진트리(Full Binary Tree)란?
- 모든 레벨이 꽉 차있는 트리의 모습

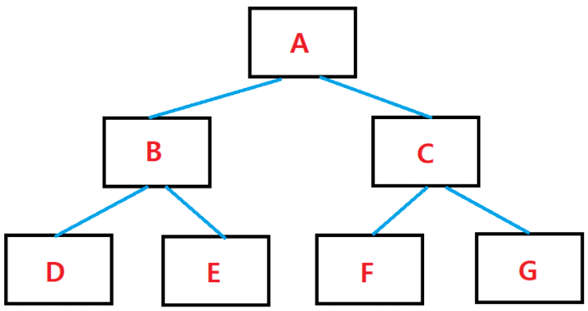
완전 이진트리(Complete Binary Tree)란?
- 완전 이진트리는 모든 레벨이 꽉차 있는 건 아니지만 위에서부터 아래로, 왼쪽부터 오른쪽으로 노드가 채워진 트리를 뜻함
- 여기서 F가 없어져도 완전 이진트리, F,E가 없어져도 완전 이진트리가 됨

이진 탐색 트리의 장점
- 일반 이진 탐색은 중앙 요소를 알아야하므로 "배열"에서만 사용할 수 있다.
  - 연결 리스트는 이진 탐색 하기에 적합하지 않음
  - 또한, 배열의 크기가 변하면 안됨. 정적이어야 함.
- "이진 탐색 트리"를 사용하여 탐색하면
  1. 배열을 사용하여 탐색할 때 보다 시간 복잡도가 줄어듬 O(logN) -> 이진 탐색
  2. 동적으로 데이터 집합 크기가 바뀌고 순서가 바뀌어도 문제 없다

이진 탐색 트리의 단점
- 트리 모양이 이렇게 한쪽으로 치우쳐지게 되면 트리 탐색의 장점인 O(logN) 시간복잡도가 마치 배열을 순차탐색 하듯 하는 O(N)에 가까워지게 된다. 이진 탐색 트리 모양이 이렇게 되면 트리 사용하여 이득보는게 없다.
- 따라서 이진 탐색 트리에 데이터를 "추가/삭제" 할 때 트리 모양이 한쪽으로 치우쳐지지 않고 균형있는 모양을 유지시키면 O(N)이 되는 것을 방지할 수 있다. -> 이렇게 균형 잡힌 이진 탐색 트리가 되도록 보장하는 트리가 "레드 블랙 트리"

class Node
{
public:
    int data;
    Node* leftChild=NULL;
    Node* rightChild=NULL;
    
    Node(int _data, Node* _leftChild, Node* _rightChild)
    	:data(_data), leftChild(_leftChild), rightChild(_rightChild)
     { }
};

// 트리에 target이 있다면 true 리턴
bool BST_SearchNode(Node* tree, int target)
{

	if(tree==NULL)
    	return false;
        
    if(tree->data == target)
    	return true;
    else if (tree->data > target)
    	return BST_SearchNode(tree->leftChild, target);
    else if (tree->data < target)
    	return BST_SearchNode(tree->rightChild, target);
}

// 트리에 target이 있다면 해당 노드 리턴
Node* BST_SearchNode(Node* tree, int target)
{
	if(tree==NULL)
    	return NULL;
        
    if(tree->data ==target)
    	return tree;
    else if(tree->data > target)
    	return BST_SearchNode(tree->leftChild, target);
    else if(tree->data < target)
    	return BST_SearchNode(tree->rightChild, target);
}

tree를 루트로 하는 서브트리로 재귀호출을 하면서 내려온다

- 왼쪽 서브 트리의 루트로 호출하면 왼쪽으로 내려가는 것이고

- 오른쪽 서브 트리의 루트로 호출하면 오른쪽으로 내려가는 것이 된다

void BST_InsertNode(Node* tree, Node* node)
{
	if(node->data<tree->data) //현재 재귀 단계에서의 트리의 루트와 크기 비교(서브트리의 루트)
    {
    	if(tree->leftChild == NULL) //루트보다 작은데 마침 루트에게 왼쪽 자식이 없다면 루트의 왼쪽 자식으로 세팅 후 종료  
        {
        	tree->leftChild=node;
        	return;
        }
        else
        	BST_InsertNode(tree->leftChild, node); // 루트보다 작은데 루트에게 왼쪽 자식이 있다면 거기에 추가될 수 없으므로 더 내려가야 함   
    
    }
    else if (node->data > tree->data) //루트보다 큰데 마침 루트에게 오른쪽 자식이 없다면 루트의 오른쪽 자식으로 세팅 후 종료 
    { 
       if(tree->rightChild ==NULL)
       {
           tree->rightChild=node;
           return;
       }
       else
   	      BST_InsertNode(tree->rightChild, node); //루트보다 큰데 루트에게 오른쪽 자식이 있다면 거기에 추가될 수 없으므로 더 내려가야 함

	}

}

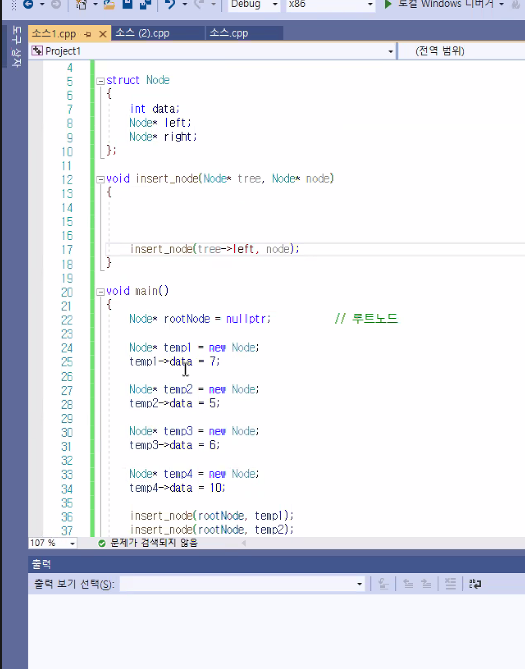
Insert_node(Node* tree, Node* node 트리에 노드 하나를 만들어준다)

tree는 실제 있는 트리이고 node는 새로 만든 data인데

insert_node 함수 밖에 (main 등에서) 미리 만들어줘야함

Node* temp1= new Node;
temp->data=7;

삭제는 코드를 다 외운다기 보다는

한번 이해하고 넘어가기

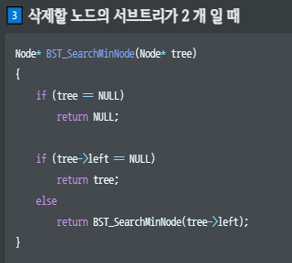
Node* BST_SearchNode(Node* tree)
{
	if (tree == NULL)
	{
		return NULL;
	}

	if (tree->left == NULL)
		return true;
	else
		return BST_SearchMinNode(tree->left);

}

Node* BST_SearchMinNode(Node* tree)
{
	if (tree == NULL)
		return NULL;

	if (tree->left == NULL)
		return tree;
	else
		return BST_SearchMinNode(tree->left);
}

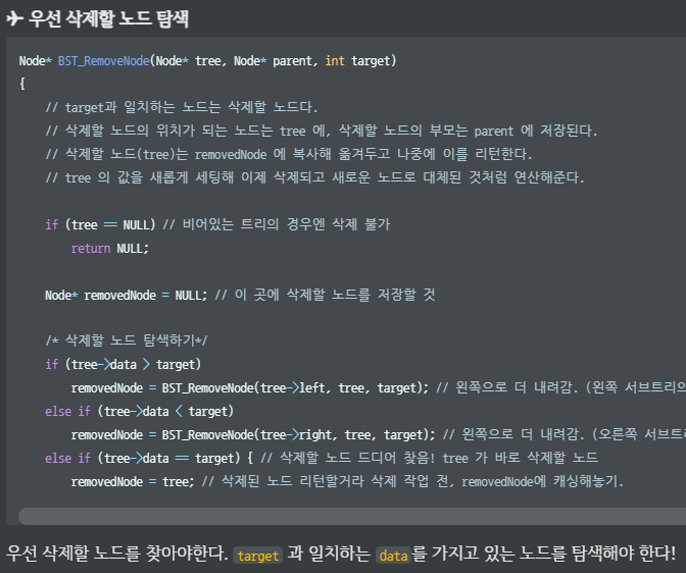
Node* BST_RemoveNode(Node* tree, Node* parent, int target)
{
	//target과 일치하는 노드는 삭제할 노드다.
	//삭제할 노드의 위치가 되는 노드는 tree에, 삭제할 노드의 부모는 parent에 저장된다.
	//삭제할 노드(tree)는 removeNode에 복사해 옮겨두고 나중에 이를 리턴한다.
	//tree의 값을 새롭게 세팅해 이제 삭제되고 새로운 노드로 대체된 것처럼 연산해준다.

	if (tree == NULL) //비어있는 트리의 경우엔 삭제 불가
		return NULL;

	Node* removeNode = NULL; //이 곳에 삭제할 노드를 저장할 것

	/* 삭제할 노드 탐색하기 */
	if (tree->data > target)
		removeNode = BST_RemoveNode(tree->left, tree, target); //왼쪽으로 더 내려감
	else if (tree->data < target)
		removeNode= BST_RemoveNode(tree->right, tree, target); //오른쪽으로 더 내려감
	else if (tree->data == target) { //삭제할 노드 드디어 찾음! tree가 바로 삭제할 노드
		removeNode = tree;

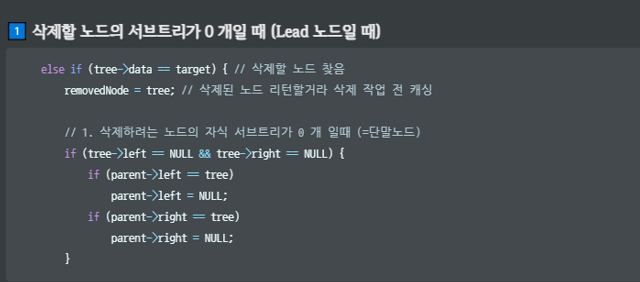
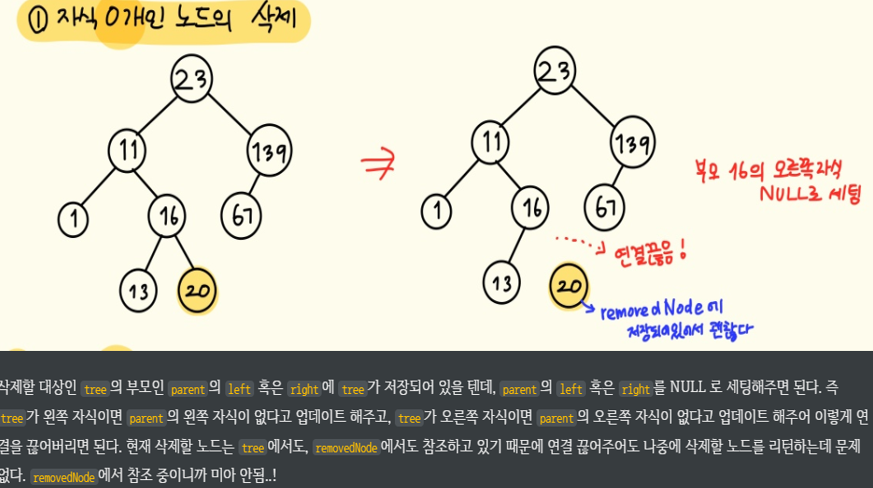
		// 1. 삭제하는 노드의 자식 서브트리가 0개일 때(=단말노드)
		if (tree->left == NULL && tree->right == NULL)
		{
			if(parent->left == tree)
				parent->left == NULL;
			if(parent->right == tree)
				parent->right = NULL;
		}
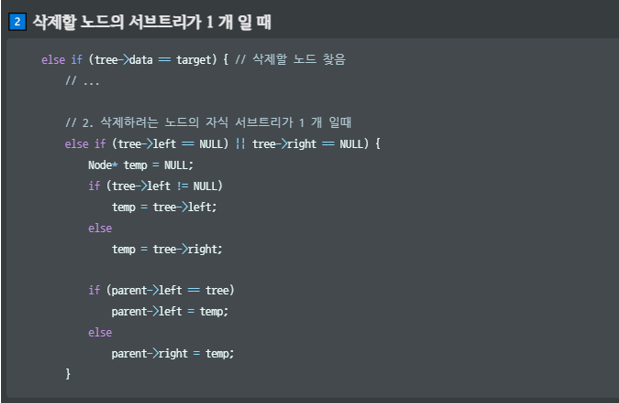
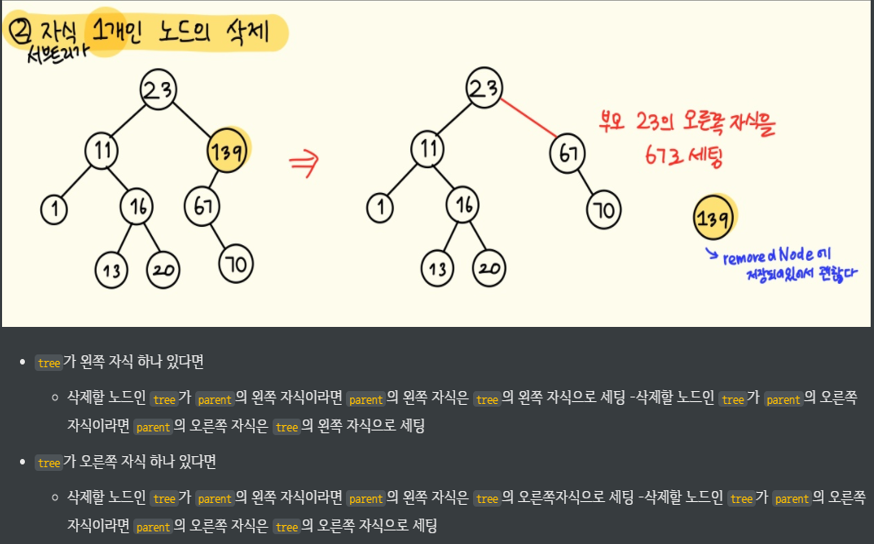
		// 2. 삭제하려는 노드의 자식 서브트리가 1개일 때
		else if (tree->left == NULL || tree->right == NULL)
		{
			Node* temp = NULL;
			if (tree->left != NULL)
				temp = tree->left;
			else
				temp = tree->right;

			if (parent->left == tree)
				parent->left = temp;
			else
				parent->right = temp;
		}
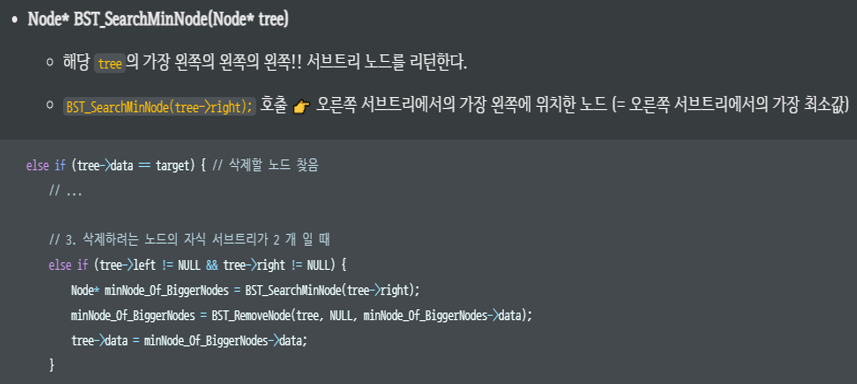
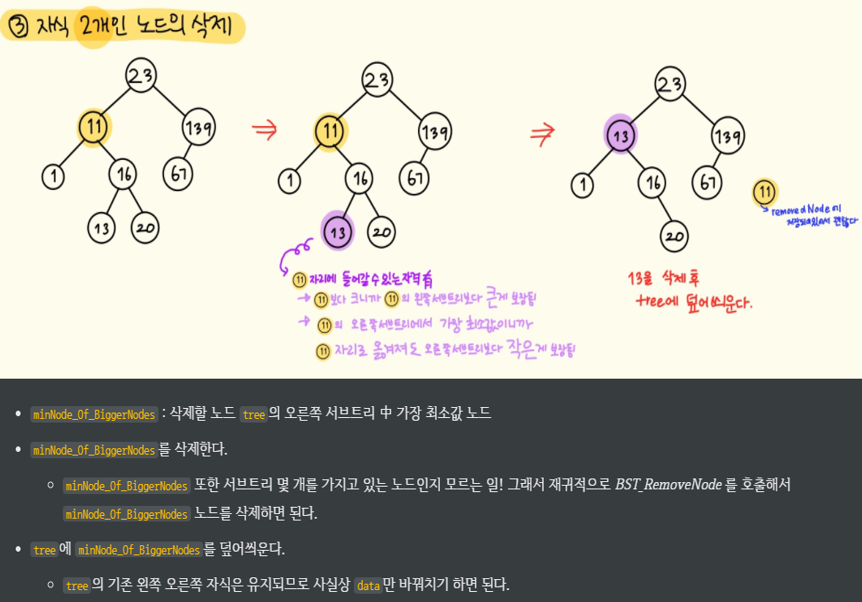
		// 3. 삭제하려는 노드의 자식 서브트리가 2개일 때
		else if (tree->left!=NULL && tree->right!=NULL) { 
			Node* minNode_Of_BiggerNodes = BST_SearchMinNode(tree->right);
			minNode_Of_BiggerNodes = BST_RemoveNode(tree, NULL, minNode_Of_BiggerNodes->data);
			tree->data = minNode_Of_BiggerNodes->data;
		}

	}
	return removeNode;
}

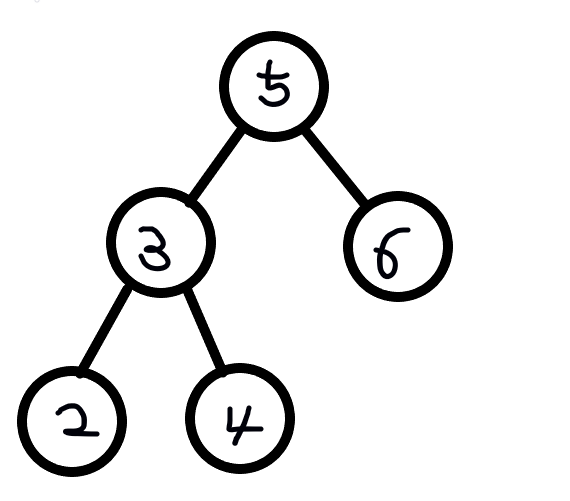
순회

전위 순회
- 내려가기 전 출력 (두 서브트리 순회 전)

void BST_PreOrder(Node* tree, vector<int>& pre)
{
    if(tree==NULL)
        return;
    pre.push_back(tree->data); //출력
    BST_PreOrder(tree->leftChild, pre);
    BST_PreOrder(tree->rightChild, pre);
}

답: 5-3-2-4-6

중위 순회
- 왼쪽 서브트리 순회 전부 마치고 돌아온 후 출력 후 오른쪽 서브트리 순회
이진 검색 트리를 '중위 순회' 하면 정렬된 순서대로 출력이 된다

void BST_InOrder(Node* tree, vector<int>& pos)
{
    if(tree=NULL)
        return;
    
    BST_InOrder(tree->leftChild, pos);
    pos.push_back(tree->data); //출력
    BST_InOrder(tree->rightChild, pos);
    
}

답: 2-3-4-5-6

후위 순회
- 왼쪽 서브트리 순회, 오른쪽 서브트리 순회 전부 다 마치고 돌아온 후에 출력

void BST_PostOrder(Node* tree, vector<int>& pos)
{
    if(tree==NULL)
        return;
    BST_PostOrder(tree->leftChild, pos);
    BST_PostOrder(tree->rightChild, pos);
    pos.push_back(tree->data); //출력
}

답: 2-4-3-6-5

수식트리
- 수식트리 조건
  - 피연산자는 잎 노드
  - 연산자는 루트 노드 또는 가지 노드

3*4 + (6-8) 수식을 이진 트리로 표현하면 다음과 같음

'3 4 * 6 8 - +' 수식을 트리로 구축하는 과정(후위순회)

1. 가장 마지막인 '+' 연산자가 루트 노드가 된다.

2. 다음 토큰으로 '-' 연산자를 읽어 루트노드의 왼쪽 자식 노드가 된다.

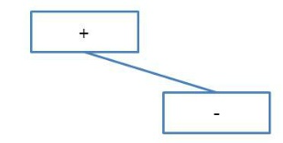
3. 다음 토큰 두개는 숫자(피연산자)이므로 각각 '-' 노드의 양쪽 자식이 된다

4. 다음 토큰으로 '*'(연산자)로 루트 노드인 '+' 노드의 왼쪽 자식 노드가 된다.

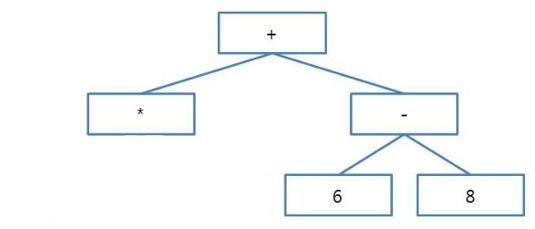
5. 나머지 토큰인 숫자(피연산자)는 '*' 노드의 양쪽 자식 노드가 된다.

'C++' 카테고리의 다른 글

#10. 네트워크 (0)	2022.05.16
#7. STL , - Vector (0)	2022.04.28
[C++] 상속, 생성자/소멸자 호출 순서, 다형성, 정적/동적 바인딩, 가상 소멸자 (0)	2022.03.09
[C++] 복사 생성자, 함수 오버로딩, 연산자 오버로딩, friend 키워드 (0)	2022.02.25
#4. cast, dynamic_cast, RTTI, friend 클래스 (0)	2022.02.19

매번 그때는 모를 뿐이다

#5. 자료구조

'C++' 카테고리의 다른 글

댓글

티스토리툴바

#5. 자료구조

'C++' 카테고리의 다른 글

관련글

댓글

티스토리툴바