쿼터니언과 3차원 회전 | Quaternion | 사원수 - YouTube
쿼터니언
그래픽스나 로보틱스에서 3차원 회전을 표현할 때 많이 사용함
특히 캐릭터 애니메이션 같은 경우 각 관절들이 상대적인 회전을 표현할 때 필수적으로 사용됨
3차원 회전은 3자유도
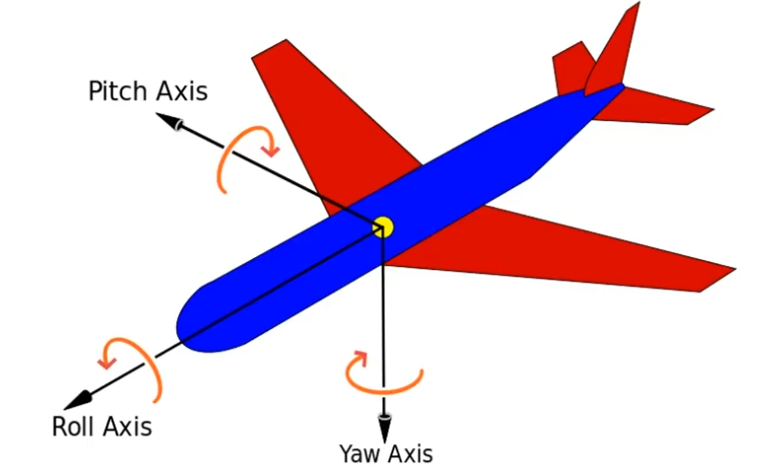
Gimbal Lock
회전을 표현하려면 3자유도가 필요한데 앵글들이 조합이 잘못되면 자유도 하나가 사라져버려서 표현력이 떨어져버림
Euler (gimbal lock) Explained - YouTube
쿼터니언
쿼터: 4. 4원수
- 쿼터니언은 복소수를 확장한 x, y, z, w 성분을 갖는 4차원 벡터로 세 개의 축을 동시에 회전시켜 축에 대한 종속 관계를 없앴으며 하나의 축이 소실되는 문제점을 방지할 수 있다.
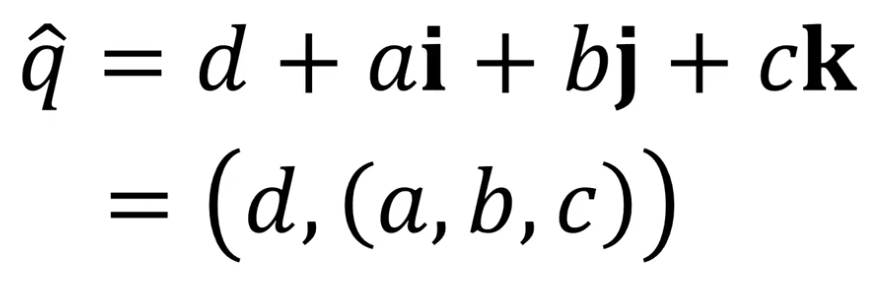
a, b, c 뒤에 i, j, k는 허수
얘를 표현을 할 때 a, b, c를 묶어서 vector 하나로 표현함
4자유도로 볼 수도 있고 뒤에 괄호를 보면 스칼라 하나 3차원 벡터 하나로 볼 수 있음
쿼터니언과 회전
3차원에서 회전을 표현할 때는 회전 축과 회전 각을 이용해서 하나의 회전을 표현함
이때 회전축은 3차원 벡터고 회전각은 스칼라 하나니까 4자유도가 됨
이 때 제약조건이 하나 더 붙게 되는데 회전축 벡터의 절댓값이 1이어야 함
1이면 유닛 쿼터니언이 됨

쿼터니언 왜 써?
마우스 이용해서 FPS 같은 경우 시점 조작할 때 회전을 반복해서 하게 되는데
이때 쿼터니언에 쿼터니언 곱하며 회전을 누적시킬 수 있다.
4 x 4 메트릭스 곱하는거나 그중에서 로테이션 메트릭스만 빼내서 곱한다고 쳐도
3 x 3 메트릭스 두개 곱하는건데
쿼터니언은 그거에 비해 속도가 빨라서 더 많이 씀
단순히 짐벌락 문제 없는 것 말고도 속도가 빨라서

쿼터니언을 이용해서 점 하나를 회전시킬 수 있다
내부적으로 구현된걸 보면 켤레복소수가 들어가있다
그래픽스 파이프라인에서는 내부적으로는 쿼터니언을 사용하고 있더라도 결국 그래픽스 파이프라인에 들어갈때는(GPU로 보내줄 때는) 결국 transformation matrix를 하나 만들어서 보내줌
그래서 쿼터니언 회전을 다시 회전 메트릭스로 만들어서 model transformation matrix나 view transformation matrix와 같이 변환을 합쳐서 그래픽스 파이프라인에 넣게 된다
Spherical Linear Interpolation
쿼터니언 두개를 Interpolation 시켜야 할 때가 있음
예를 들어 캐릭터 애니메이션을 하는데 두 시점에 대해 쿼터니언 두개가 따로 있으면
두 키프레임 사이에 어떤 동작을 표현하고 싶다면 Interpolation을 많이 사용함
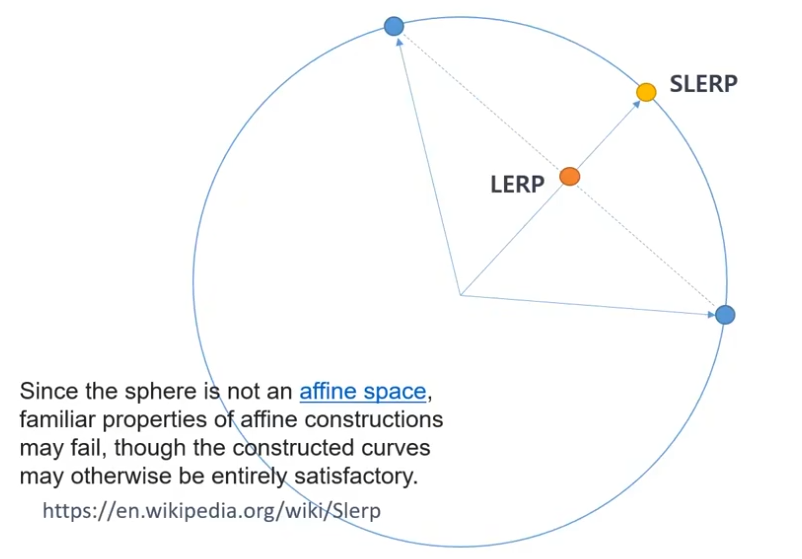
쿼터니언을 우리가 보통 사용하는 Linear Interpolation으로 Interpolation을 시켜버리면
회전을 표현하는 구 위로 떨어지는게 아니고 unit length constraint가 깨지면서(SLERP) 안쪽으로 들어와버림(LERP)
이때 LERP를 밖으로 다시 빼는 방법도 있겠지만
보통 Spherical Linear Interpolation을 사용해서 Interpolation된 결과가 항상 Sphere 위에 있도록 하는 (SLERP) 방법을 사용함
'그래픽스ㆍDirectX' 카테고리의 다른 글
| 그래픽스 파이프라인 (Graphics Pipeline) (0) | 2022.05.21 |
|---|---|
| DirectX와 OpenGL (0) | 2022.05.21 |
| 렌더링 파이프라인 - 래스터라이저와 프래그먼트 셰이더 (0) | 2022.05.21 |
| 렌더링 파이프라인 - 정점 조립과 정점 변환 (0) | 2022.05.20 |
| 셰이더 (0) | 2022.05.20 |



댓글